Site of the Gleaners who think the universe is a spherical surface
in maybe four-dimensional space
6. A mathematical formulation of the closed universe model (Appendix)
Robot: The
subject of this meeting is to present a mathematical formulation of our closed
universe mode, because it seems to be a little hard to understand what in the
observable world corresponds to the surface of a sphere in 4-dimensional space
without using mathematical formulations.
In this Homepage we use the mathematical definition about the surface of
a sphere (including inside part) or ball, that is, ‘n-sphere’ denotes the surface of a ball in (n+1)-dimensional space. In short, ‘n-sphere’ denotes the n-dimensional spherical surface.
Stamp Pony: It
is a little confusing.
Glass Snake: In
other words, n-sphere denotes the surface of a circle or ball, where the
position of any point on the surface can be determined uniquely by n parameters.
This means that an ordinary n-sphere is n-dimensional space. However, as will
be explained bellow, the universe is an exception. Since we can recognize many
rings (1-spheres) and many spherical surfaces (2-spheres) in this observable
world, there can exist 1-spheres, 2-spheres, …, and
(n-1)-spheres in n-dimensional space,
Robot: And, if
we use a coordinate system with X, Y, Z axes, (x, y, z)
denotes the coordinate of a point in the coordinate system.
Glass Snake: Let's start by reviewing a simple case. Robot, would you mind explaining
the case of a 2-sphere?
Robot: My policy is not to do what humans can do. P. Sheep, it's your turn.
Puzzle Sheep: Let
us suppose that there is 2-sphere S2 of radius R in 3-dimensional (3-d) space
as shown in Fig. 9A. Then we set observing point OP at an end (e.g. South Pole)
of S2, and its conjugate point CP at the opposite end (e.g. North Pole) of S2.
We then define a 3-d rectangular coordinate system with X, Y,
H axes whose origin O is at the center of S2, where H-axis denotes a straight
line passing observing point OP and its conjugate point CP, and X, Y axes are
perpendicular to H-axis.
Stamp Pony: It
seems to me that H-axis means Hubble axis or Great Bull axis.
Puzzle Sheep: We then define a two dimensional (2-d) observing coordinate with X' and
Y' axes whose origin is at observing point OP, where X' and Y' axes are
set along S2 (spherical surface) and are perpendicular with each other
at observing point OP. The 2-d observing coordinate system is used by 2-d
observers living on S2. The 2-d observers' world can be called the 2-d
observable world. Although X' and Y' axes are curved in 3-d space, those
axes seem to be straight lines for 2-d observers.
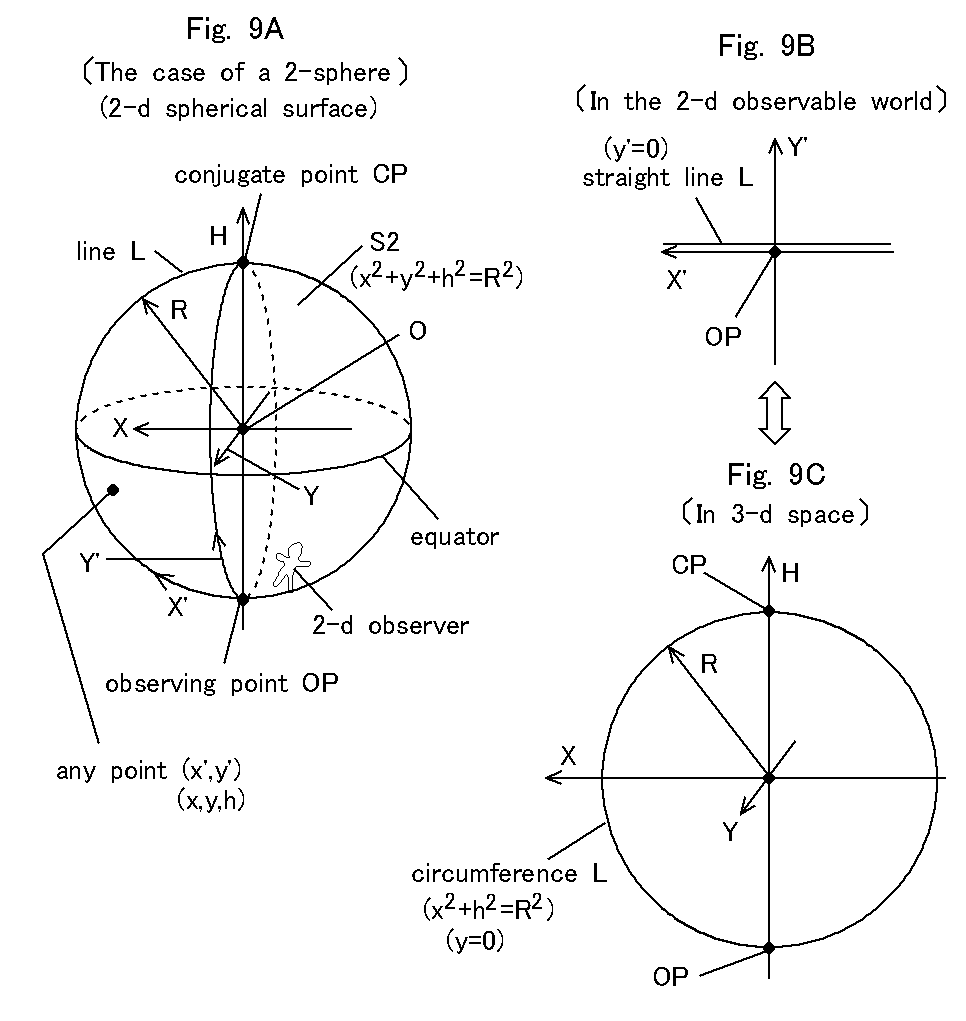
The coordinate of a point on S2 is expressed by (x, y, h) in the 3-d coordinate
system and (x', y') in the observing coordinate system. The coordinate
of observing point OP is (0, 0, -R) or (0, 0) and that of its conjugate
point CP is (0, 0, R) or (±πR, ±πR). The equation for S2 is written as
x2+y2+h2=R2. (1)
Here we can suppose that X'-axis and Y'-axis exist on XH
plane and YH plane, respectively, in the 3-d coordinate system. This means that X'
and Y' axes are parallel to X and Y axes, respectively at the observing
point OP. This also means that about the coordinate of any point on S2
if x' is 0, then x is 0, and if y' is 0, then y is 0. Then on the one hand,
line L whose Y' coordinate is 0 (y'=0 and y=0) in Fig. 9A seems to be a
straight line passing observing point OP along X'-axis in the 2-d observable
world as shown in Fig. 9B. But, on the other, the line L corresponds to
a circumference (y=0) of radius R on XH
plane in 3-d space as shown in Fig. 9C, since if we take y=0 in Eq. (1), we obtain the following equation expressing a
circumference:
x2+h2=R2. (2)
Stamp Pony:
From your explanation I see that each straight line in the 2-d observable world
corresponds to a circumference (ring or 1-sphere) in 3-d space.
Robot: In other
words, a ring (1-sphere) is a cross section of 2-sphere, and 2-sphere is a set
of many rings (1-spheres), where these rings can be obtained by rotating a ring
around an axis (e.g. H-axis in the case of Fig. 9C).
Glass Snake:
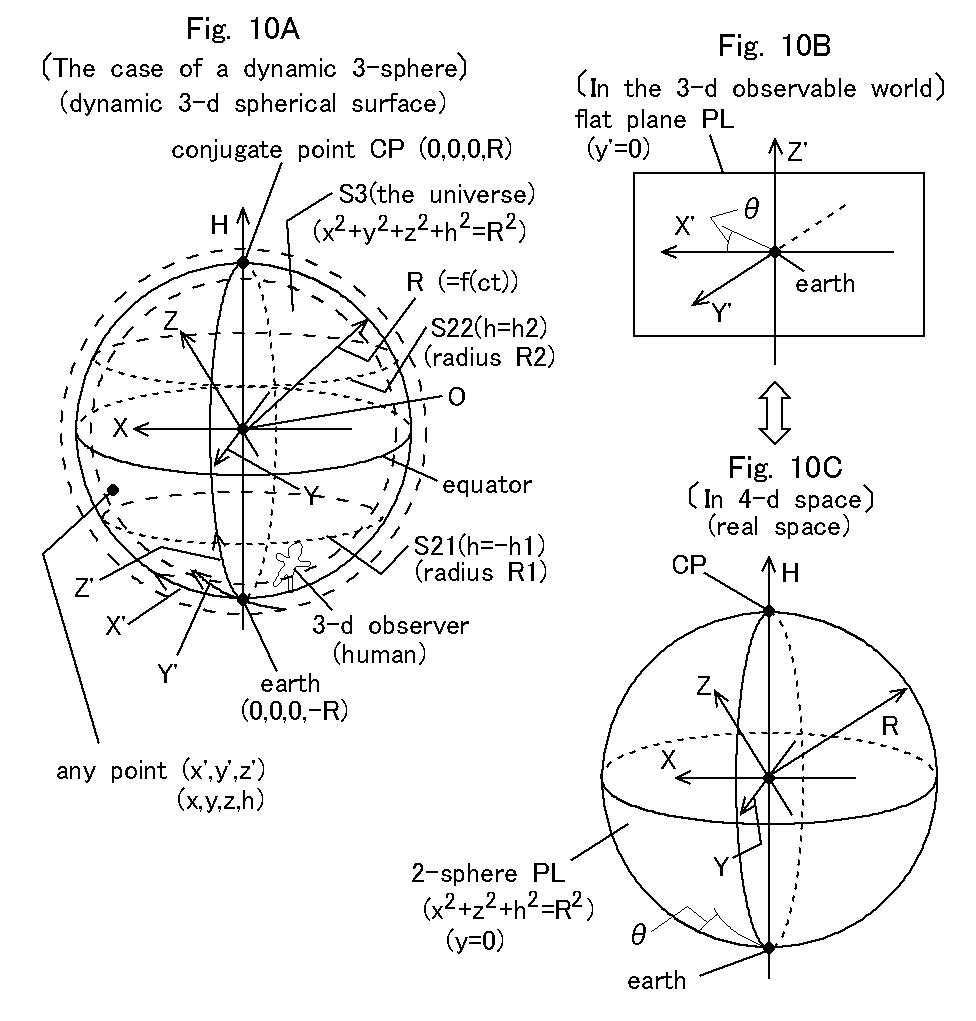
Here we extend the above arguments to the case of a 3-sphere, i.e. our closed
universe model. Let us suppose
that there is 3-sphere S3 (the universe) of radius R in 4-dimensional (4-d)
space as shown in Fig. 10A. Since radius R is expanding, 3-sphere S3 is called
a dynamic one. Then we set the position of the earth (observing point) at an
end (e.g. South Pole) of S3, and its conjugate point CP at the opposite end
(e.g. North Pole) of S3. We then define a 4-d rectangular (Euclidean)
coordinate system with X, Y, Z, H axes whose origin O is at the center of S3,
where H-axis (Hubble axis) denotes a straight line passing the earth and its
conjugate point CP, and X, Y, Z axes are perpendicular to H-axis.
Stamp Pony: It
seems to me that Z-axis is not perpendicular to X, H axes.
Glass Snake: We cannot express the 4-d coordinate system in this 3-d observable world
correctly. We then define a three dimensional (3-d) observing coordinate
with X', Y', and Z' axes whose origin is at the earth, where X', Y', and
Z' axes are set along S3 (dynamic spherical surface) and are perpendicular
with one another at the earth. The 3-d observing coordinate system is used
by 3-d observers (humans) living on or in S3. The 3-d observers' world
can be called the 3-d observable world. Although X', Y', and Z' axes are
curved in 4-d space, those axes seem to be straight lines for 3-d observers.
The coordinate of a point on S3 is expressed by (x, y, z, h) in the 4-d
coordinate system and (x', y', z') in the observing coordinate system.
The coordinate of the earth is (0, 0, 0, -R) or (0, 0, 0) and that of its
conjugate point CP is (0, 0, 0, R) or (±πR, ±πR, ±πR). The equation for S3 is written as
x2+y2+z2+h2=R2, (3)
R=f (ct).
(4)
Eq. (4) means that the radius R of S3 is a function f of
ct, where c is the speed of light and t is time. In short, the radius R is a
function of time.
If
the universe is expanding at the speed of light, f (ct) is ct/π. If not, f (ct) is more complicated. Since
radius R is expanding, the dynamic 3-sphere S3 (the universe) is 4-dimensional
space including time dimension. So is the 3-d observable world.
Robot: If the expanding speed of the universe is constant, the universe may be
just expanding according to the Newton's first law of motion and it may
be an inertial frame. If not, the universe may not necessarily be an inertial
frame. Here, we'd better not ask G. Snake where the time t is defined about Eq.
(4).
Glass Snake: A very good point! I think the time t is defined at the earth (any observing
point). The fact that radius R is a function of time means that radius
R is distant dimension as well as being time dimension. If S3 (the universe)
is constructed in four distant dimension space, we need one more dimension,
i.e. time dimension, to enable us to move. However since radius R is mixed
dimension of distance and time, we don't necessarily need five dimensions.
Puzzle Sheep: You
mean that at least the macroscopic structure of the universe (S3) seems to be
constructed in 4-d space including time dimension.
Glass Snake: That's right. Then by analogy of the case of 2-sphere, we suppose that
we can set the observing coordinate system so that X', Y', and Z' axes
are parallel to X, Y, and Z axes, respectively at the earth. This means
that about the coordinate of any point on S3 if y' is 0, then y is 0. Then
on the one hand, plane PL whose Y' coordinate is 0 (y'=0 and y=0) in Fig.
10B seems to be a flat plane passing the earth in the 3-d observable world
for 3-d observers. But, on the other, the plane PL corresponds to a 2-sphere
of radius R in 4-d space as shown in Fig. 10C, since if we take y=0 in
Eq. (3),
we obtain the following equation expressing a 2-sphere:
x2+z2+h2=R2. (5)
Stamp Pony:
Then each plane in the 3-d observable world corresponds to a 2-sphere
(spherical surface) in 4-d space. Thus in the previous meetings we used only
the optical properties of 2-sphere.
Robot: In other
words a 2-sphere is a cross section of 3-sphere S3. And S3 is a set of many
2-spheres, where these 2-spheres may be obtained by rotating a 2-sphere around
an axis.
Glass Snake: Then if we take h=-h1 (-R<-h1<=0) in Eq. (3), we obtain
the following equation expressing 2-sphere S21 as shown in Fig. 10A:
x2+y2+z2+h12=R2 or x2+y2+z2
=R2 -h12. (6)
The
radius R1 of S21 is expressed as
R1= (R2 -h12)1/2 . (7)
Furthermore
if we take h=h2 (0<h2<R) in Eq. (3), we obtain
the following equation expressing 2-sphere S22:
x2+y2+z2+h22=R2 or x2+y2+z2
=R2 -h22. (8)
The
radius R2 of S22 is expressed as
R2= (R2 -h22)1/2 . (9)
The
2-sphears S21 and S22 are cross sections of S3. It should be noted that if
h1=h2, then R1=R2. Here, S. Pony, would you mind explaining how 2-sphears S21
and S22 look like from the earth in the 3-d observable world?
Stamp Pony: The
distance between the earth and every point on 2-sphear S21, or the radius r1 of
S21 in the 3-d observable world is R·arcos (h1/R),
where arcos means arc cosine. The 2-sphear S21 appears to be a spherical
surface of radius r1 whose center is at the earth for 3-d observers on the
earth as shown in Fig. 11A. Similarly, the 2-sphear S22 appears to be a
spherical surface of radius r2 whose center is at the earth as shown in Fig. 11B,
where r2 is R{π-arcos(h2/R)}.
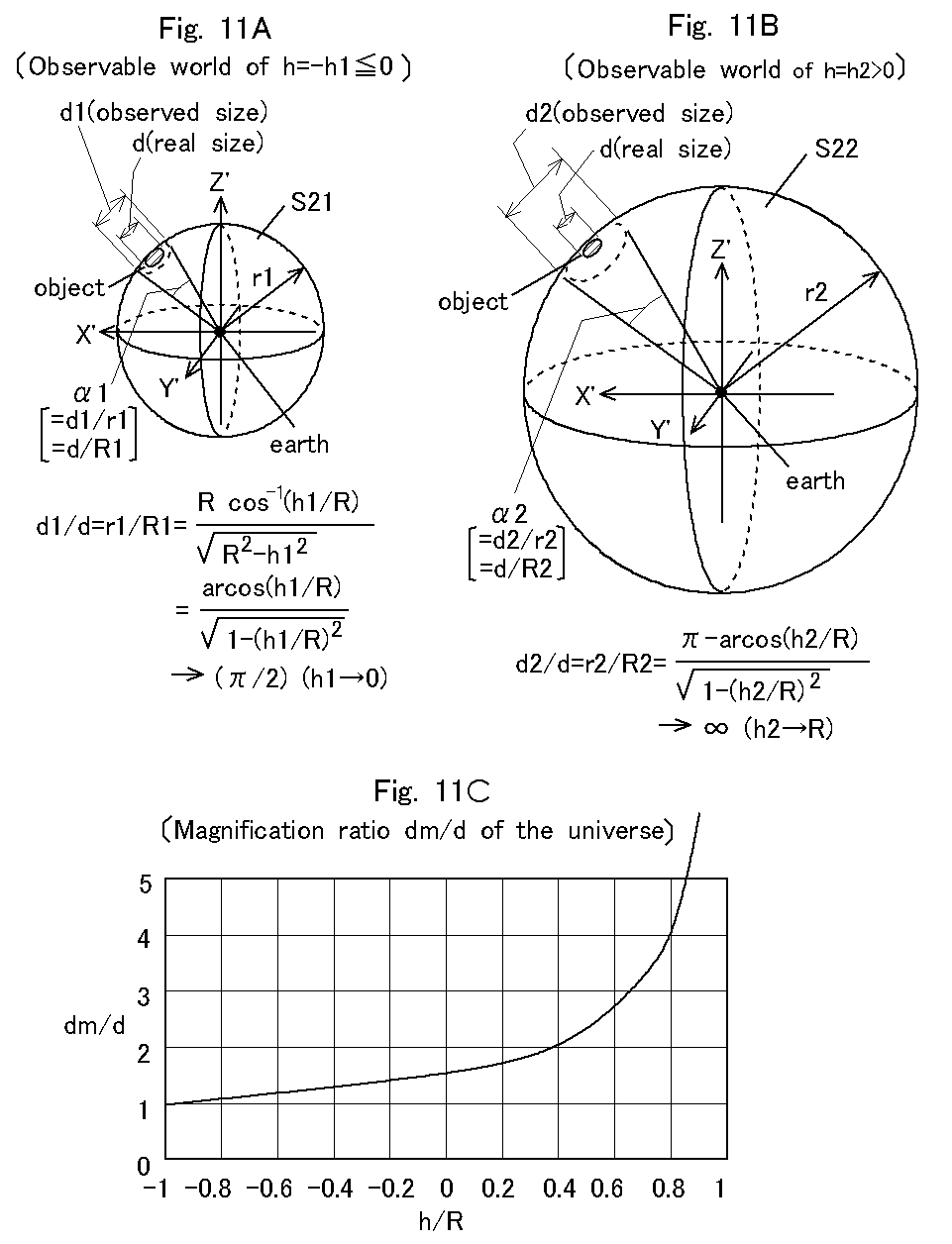
d1/d =r1/R1 = R•arcos (h1/R)/ (R2 -h12)1/2
= arcos (h1/R)/ {1 - (h1/R)2}1/2 . (10)
Then if an object of diameter d exits on S22, the diameter of the object
seems to be d2 which is larger than d and d1 from the earth, where the
magnification ratio d2/d is expressed as
d2/d =r2/R2 = R{π-arcos (h2/R)}/ (R2 –h22)1/2
= {π-arcos (h2/R)}/ {1 - (h2/R)2}1/2
. (11)
Then if we express the magnification ratio dm/d as the function of h/R,
where dm is the observed diameter and h is the H-axis coordinate, we obtain
the graph of Fig. 11C. The nearer h/R draws close to 1, the higher the
magnification ratio becomes.
Robot: Well
done! As for view angles, the observed angle α1 of the object on S21 is d1/r1
or d/R1, and the angle α2 of the object on S22 is d2/r2 or d/R2. It should be noted
that if h1=h2, then the observed angles of the objects of the same size on S21
and S22 are the same.
Puzzle Sheep: In
this sense, we can say that the 2-sphere S21 of h=-h1 is equivalent to the
2-sphere S22 of h=h1. Then we have yet to study the optical properties of the dynamic
3-sphere S3.
Robot: I shall
ask you to close the meeting now.
All: We are
spherical-surfacelings! We are the Gleaners!
Robot: In Mr. Spoch or
Leonard Nimoy accent!
All: (With
Vulcan salute sign) Nice to meet you, we are the Gleaners! Live long and prosper!
Robot: You,
maybe better called surfacebeings! Dismissed!
Latest update: 2016/1/4
A
narrow and maybe insecure path to the Gleaners:
(Mail
to: o-pat-consulting@hotmail.co.jp)
Historical first meeting of the Gleaners: A simple reason why the
universe seems to be closed