The Schmidt theory is one of the isothermal calculation methods for Stirling engines. It is the most simple method and very useful during Stirling engine development.
This theory is based on the isothermal expansion and compression of an ideal gas.

The performance of the engine can be calculated a P-V diagram. The volume in the engine is easily calculated by using the internal geometry. When the volume, mass of the working gas and the temperature is decided, the pressure is calculated using an ideal gas method as shown in equation (1).

(1)

The engine pressure can be calculated under following assumptions:
(a) There is no pressure loss in the heat-exchangers and there are no internal pressure differences.
(b) The expansion process and the compression process changes isothermal.
(c) Conditions of the working gas is changed as an ideal gas.
(d) There is a perfect regeneration.
(e) The expansion dead space maintains the expansion gas temperature - T_E, the compression dead space maintains the compression gas temperature - T_C during the cycle.
(f) The regenerator gas temperature is an average of the expansion gas temperature - T_E and the compression gas temperature - T_C.
(g) The expansion space - V_E and the compression space - V_C changes according a sine curves.

Table 1 shows symbols used the Schmidt Theory.

Figure 1 shows the calculation model of Alpha-type Stirling engine.

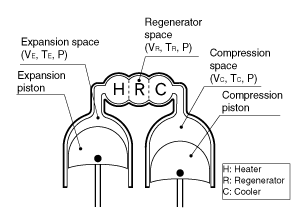
Fig. 1 Alpha-type Stirling Engine

(2)

The momental compression volume - V_C is found in equation (3) with a swept volume of the compression piston - V_SC, a compression dead volume - V_DC and a phase angle - dx.

(3)

The total momental volume is calculated in equation (4).

(4)

By the assumptions (a), (b) and (c), the total mass in the engine - m is calculated using the engine pressure - P, each temperature - T , each volume - V and the gas constant - R.

(5)

The temperature ratio - t, a swept volume ratio - v and other dead volume ratios are found using the following equations.

(6)

(7)

(8)

(9)

(10)

The regenerator temperature - T_R is calculated in equation (11), by using the assumption (f).

(11)

When equation (5) is changed using equation (6)-(10), the total gas mass - m is described in the next equation.

(12)

Equation (12) is changed in equation (13), using equation (2) and (3).

(13)

Now;

(14)

(15)

(16)

The engine pressure - P is defined as a next equation using equation (13).

(17)

The mean pressure - P_mean can be calculated as follows:

(18)

c is defined in the next equation.

(19)

As a result, the engine pressure - P, based the mean engine pressure - P_mean is calculated in equation (20).

(20)

On the other hand, in the case of equation (17), when cos(x-a)=-1, the engine pressure - P becomes the minimum pressure - P_min, the next equation is introduced.

(21)

Therefore, the engine pressure - P, based the minimum pressure - P_min is described in equation (22).

(22)

Similarly, when cos(x-a)=1, the engine pressure - P becomes the maximum pressure - P_max. The following equation is introduced.

(23)

The P-V diagram of Alpha-type Stirling engine can be made with above equations.

Similarly, the equations for Beta-type Stirling engine are declared. Figure 2 shows a calculation model of a Beta-type Stirling engine.

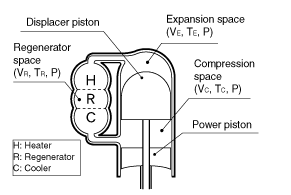
Fig. 2 Beta-type Stirling Engine

(24)

(25)

In the case of the Beta-type Stirling engine, the displacer piston and the power piston are located in the same cylinder. When both pistons overlaps there stroke, an effective working space is created. The overlap volume - V_B in equation (25) can be calculated in the next equation.

(26)

Then the total momental volume - V is found in equation (27).

(27)

The engine pressure - P based the mean pressure - P_mean, the minimum pressure - P_min and the maximum pressure - P_max are described in the following equations like the Alpha-type Stirling engine.

(28)

Several ratios and coefficients are defined as follows.

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

The P-V diagram of Beta-type Stirling engine can be made with above equations.

Figure 3 shows a calculation model of a Gamma-type Stirling engine.

Fig. 3 Gamma-type Stirling Engine

(39)

(40)

The total momental volume - V is described a next equation.

(41)

The engine pressure - P based the mean pressure - P_mean, the minimum pressure - P_min and the maximum pressure - P_max are found in the following equations.

(42)?

Now,

(43)

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

The P-V diagram of Gamma-type Stirling engine can be made with above equations.

The indicated energy (area of the P-V diagram) in the expansion and compression space can be calculated as an analytical solutions with use of the above coefficients. The indicated energy in the expansion space (indicated expansion energy) - W_E(J), based on the mean pressure - P_mean, the minimum pressure - P_min and the maximum pressure - P_max are described in the following equations.

(52)

The indicated energy in the compression space (indicated compression energy) - W_C(J) are described in the next equations.

(53)

The indicated energy per one cycle of this engine - W_i(J) is demanded in the next equations.

(54)

Relations between P_mean, P_min and P_max are determined in the following equations.

(55)

(56)

The indicated expansion power - L_E(W), the indicated compression power - L_C(W) and the indicated power of this engine - L_i(W) are defined in the following equations, using the engine speed per one second , n(rps, Hz).

(57)

(58)

(59)

The indicated expansion energy - W_E found equation (52) means an input heat from a heat source to the engine. The indicated compression energy - W_c calculated by equation (53) means a reject heat from the engine to cooling water or air. Then the thermal efficiency of the engine - e is calculated in the next equation.

(60)

This efficiency equals that of a Cornot cycle which is the most highest efficiency in every thermal engine.

Make a P-V diagram and calculate the indicated power of an Alpha-type Stirling engine under following conditions.
Swept volume of an expansion piston: 0.628 cm³, swept volume of a compression piston: 0.628 cm³, dead volume of the expansion space: 0.2cm³, dead volume of the compression space: 0.2cm³, regenerator volume: 0.2cm³, phase angle: 90deg, mean pressure: 101.3 kPa, expansion gas temperature: 400degC, compression gas temperature: 30degC, engine speed: 2000 rpm.

A temperature ratio - t, a swept volume ratio - v and other dead volume ratio are calculated with the equation (6) - (10).

Each coefficient is calculated with equation (14) - (16) and (19).

Engine pressure is calculated with equation (20).

When crank angle - x=0deg:

Similarly, when x=10deg:

When x=20deg:

�c

Next each momental volume is calculated with equation (2) - (4).
When crank angle, x=0deg:

When x=10deg:

When x=20deg:

�c

Repeat above calculation to one complete cycle and plot the volumes - V and pressures - P on a graph paper.
An example of the P-V diagram is shown in Fig. 4.

Fig. 4 P-V Diagram

The indicated power of this engines is calculated with equation (59).

The indicated power of this engine is 0.689 W.

I wish to thank J. H. de Baat for many helpful suggestions during the translation of this script.

1) G. Walker., Stirling Engines, (1980),17, Oxford Univ. Press.

Return to Stirling Engiene Home Page Academic Edition